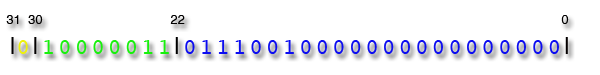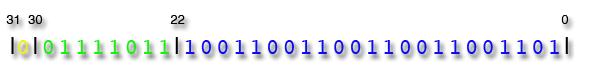Inhaltsverzeichnis
Gleitkommazahlen
Bislang dachte ich, dass Rechnen alles ist was Computer können und das obendrein noch richtig schnell aber das dem offensichtlich nicht so ist, habe ich beim Erlernen meiner ersten Programmiersprache (C) doch recht schnell herausgefunden. Schon beim studieren der Datentypen bin ich sehr rasch auf einige Unregelmäßigkeiten gestoßen.
Das Problem
Das Problem über das ich gestolpert bin, sind Berechnungen mit Gleitkommazahlen, auch Floating Points genannt. Der scheinbare Übersetzungsfehler von »Point« zu »Komma« kommt daher, dass im amerikanischen Zahlensystem der »Punkt« als Dezimaltrennzeichen verwendet wird. Fragt man nun einen Computer ob »0,1 + 0,1 + 0,1« gleich »0,3« oder »1,1 * 1,1« gleich »1,21« ist, sagt er Nein. Klingt komisch, ist aber so:
float_1.c
#include <stdio.h> int main( void ) { printf( "%d\n", 1.1 * 1.1 == 1.21 ); printf( "%d\n", 0.1 + 0.1 + 0.1 == 0.3 ); }
Dieses Programm vergleicht mit dem Vergleichsoperator »==« ob die Gleichungen in der printf-Anweisung wahr oder falsch sind, wobei eine »1« als Rückgabe die Gleichung als »wahr«, bzw. eine »0« die Gleichung als »falsch« identifiziert:
$ ./float_1
0
0
Da hat mein Weltbild schon angefangen zu wanken aber was ist dabei schlief gelaufen? Schauen wir uns mal an, was dann die og Rechnungen für ein Ergebnis liefern:
float_2.c
#include <stdio.h> float f = 0.1 + 0.1 + 0.1; float e = 1.1 * 1.1; int main( void ) { printf( "%.9f\n", f ); printf( "%.9f\n", e ); }
Dieser Code gibt die Summen der Addition bzw. Multiplikation in der Variableninitialisierung mit neun Nachkommastellen aus:
$ ./float_2
0.300000012
1.210000038
Das erklärt zumindest mal das überraschende Ergebnis der Vergleichsoperation im ersten Programm aber befriedigend ist das erst mal nicht. Das Ganze geht sogar noch einen Schritt weiter, lassen wir den Rechner mal nicht rechnen, sondern uns nur die interne Darstellung der beiden Zahlen »0,1« und »1,1« ausgeben:
float_3.c
#include <stdio.h> float f = 0.1; float e = 1.1; int main( void ) { printf( "%.9f\n", f ); printf( "%.9f\n", e ); }
$ ./float_3
0.100000001
1.100000024
Ich fand, dass schreit nach einer Erklärung und ich habe dieses Thema in der Newsgroup »de.comp.lang.c« zur Diskussion gestellt, wo ich mich an dieser Stelle schon mal bei all denen bedanke, die mir geholfen haben, das Problem zu verstehen.
Also warum ist das so? Die kurze Antwort ist: Das liegt an der Art, wie intern Dezimalzahlen bzw. reelle Zahlen in binäre Gleitkommazahlen umgerechnet werden. Wie wir oben ja schon festgestellt haben, sind sogar relativ unproblematisch erscheinende Dezimalzahlen wie zB »0,1« in der binären Darstellung ein Problem, weil aus einfachen und abbrechenden Dezimalzahlen bei der Umrechnung in Binärzahlen häufig nicht abbrechende, periodische Zahlen produziert werden. Es liegt auf der Hand, das unendlichen Zahlen bei der Berechnung und Speicherung Grenzen gesetzt werden müssen, auch bei der Speicherung von zwar endlichen aber zu langen Zahlen, kommt es ab einem gewissen Punkt zB zu Rundungsfehlern und an dieser Stelle kommt es dann häufig zu solch unerwarteten Ergebnissen, wie wir oben schon gesehen haben.
Umrechnung von Dezimalzahlen in Binärzahlen
Da in Computern nur mit Bitketten gearbeitet werden kann, versteht es sich von selbst, dass die reellen Zahlen in binäre Zahlen umgewandelt werden müssen. Dazu stehen dem Datentyp »float« vier Byte bzw. »32 Bit« zur Verfügung. Demnach stehen dem Datentyp »float« 232 darstellbare Zahlen zur Verfügung.
Die einfachste Art reelle Zahlen in binäre Zahlen umzurechnen wäre die Verwendung der »Festkommazahlen«. Bei Festkommazahlen steht das Komma an einer festen Stelle bei der Berechnung. So würde zB die Addition der dezimalen Zahlen »4,125« und »1,5« im binären System bei einer angenommenen Datenbreite von 8 Bit und vier Nachkommastellen wie folgt ablaufen:
4,125 + 1,5 = 5,625
4,125 = 0100,0010 + 1,5 = 0001,1000 -------------------- = 5,625 = 0101,1010
Die Vorkommastelle wird als ganze Zahl aus dem dezimalen System mittels dem »Modulo-2« Verfahren (Divison durch 2 mit Rest) in das binäre System übertragen, die Nachkommastelle hingegen wird umgekehrt mit »Multiplikation mit 2 und Übertrag« ermittelt. Für das og Beispiel ergibt sich dann folgende Rechnung:
Dezimal nach Binär
4 / 2 = 2 R 0 2 / 2 = 1 R 0 1 / 2 = 0 R 1↑ /* Das entspricht dem binären »100« und mit »0« aufgefüllt dann: »0100« für die Vorkommastelle */ 0,125 * 2 = 0,25 -> 0 ↓ 0,25 * 2 = 0,5 -> 0 0,5 * 2 = 1,0 -> 1 0,0 * 2 = 0,0 -> 0 /* Das entspricht dem binären »0010« für die Nachkommastelle */
Beim Umrechnen vom binären System ins dezimale, ist die Angelegenheit noch trivialer, hier wird die gesamte binäre Zahl ohne Berücksichtigung der Position des Kommas ins dezimale System umgerechnet und durch 2m geteilt, wobei »m« die Anzahl der Nachkommastellen ist:
0101,10102 ⇒ 010110102 ⇒ (9010 / 24) = 9010 / 1610 = 5,62510
Der Vorteil von Festkommazahlen ist, dass damit recht einfach gerechnet werden kann. Der Nachteil dieses Verfahrens liegt darin, dass durch die feste Position des Kommas, der Wertebereich der darstellbaren Zahlen uU stark eingeschränkt wird.
Gleitkomma-Darstellungen in binären Systemen nach IEEE 754
Bei Gleitkommazahlen steht das Komma nicht mehr an einer festen Stelle, sondern wird soweit nach links verschoben, dass nur noch eine Stelle (≠ 0) vor dem Komma übrig bleibt. Die Position des Kommas wird durch einen Exponenten festgehalten, so dass sich folgende Formel für Gleitkommazahlen ergibt:
m * be
Wobei »m« der Mantisse; »b« der Basis; und »e« dem Exponenten entspricht. Beispiele:
15000 = 1,5 * 104
15250 = 1,525 * 104
0,001 = 1 * 10-3
Dieser Vorgang wird »Normalisierung« genannt und findet so auch in wissenschaftlichen Darstellungen von besonders großen oder kleinen Zahlen statt. In Computersystemen sind für die Speicherung von gebrochenen Dezimalzahlen die Datentypen »float« und »double« vorgesehen, welche beide schon implizit die Gleitkomma-Darstellung vorsehen, wobei hier jedoch als Basis »2« verwendet wird, was aus dem binären System kommt.
In der 32 Bit Matrix eines »float« Datentyps (single precision) werden insgesamt 23 Bit für die Mantisse »m«, 8 Bit für den Exponenten »e« und 1 Bit für das Vorzeichen »v« vorgesehen, damit auch negative Zahlen dargestellt werden können:
Der Exponent
Für den Exponent »e« sind im 32-Bit Datentyp »float« 8 Bit vorgesehen. Wie wir jedoch oben bei den Beispielen zur Normalisierung schon gesehen haben, kann es bei Zahlen < 0 auch zu negativen Exponenten kommen (zB 10-3). Damit auch negative Zahlen binär dargestellt werden können, wird üblicherweise die Zweierkomplementdarstellung bei solchen Datentypen angewandt. Mit 8 Bit zB lassen sich 256 Zustände darstellen, was bei normaler, nicht vorzeichenbehafteter Interpretation den Wertebereich »0 bis 255« erschließt. Bei der Zweierkomplementdarstellung hingegen wird das höchstwertige Bit für die Speicherung des Vorzeichens verwendet (0 → positiv; 1 → negativ) und die verblieben 7 Bit (welche 128 Zustände darstellen können) markieren dann den Wertebereich von »-128 bis +127«.
Auf diese Art der Einteilung wurde aber bei der Speicherung des Exponenten bewusst verzichtet, stattdessen wird der Exponent mit einem »Bias« gespeichert. Der »Bias« ist ein vereinbarter, gedachter Wert, welcher zu dem eigentlichen Exponenten hinzu addiert wird. Der »Bias« beträgt bei »float« mit 8 Bit Exponent den Wert »127«, welcher sich nach folgender Formel errechnet (wobei »e« der Anzahl der verfügbaren Bits für die Speicherung des Exponenten entspricht):
(2(e-1)) - 1 ⇒ 27 - 1 ⇒ 128 - 1 = 127
Das Addieren der festen Zahl »127« zum Exponenten »e« bewirkt, dass der Exponent in jedem Fall positiv ist, wobei es hier einige Sonderfälle gibt, welche später noch erläutert werden.
Die Mantisse
Als »Mantisse« bezeichnet man den Bereich in welchem die normalisierte Gleitkommazahl gespeichert wird. Die Normalisierungsbedingung einer nach »IEEE 754« definierten Gleitkommazahl wurde wie folgt festgelegt:
1 ≤ m < 2
Wie oben schon erwähnt wird bei der Normalisierung einer Dezimalzahl das Komma soweit nach links verschoben, bis nur noch eine Zahl ≠ 0 vor dem Komma stehen bleibt, dieser Grundsatz gilt auch im binären System. Da es im binären System neben einer »0« nur noch eine »1« gibt, ist somit die Vorkommastelle in jedem Fall eine »1« und somit wurde in den Regularien von »IEEE 754« festgelegt, dass auf die Vorkommastelle bei der Speicherung der Mantisse verzichtet wird. Dieses Weglassen der Vorkommastelle wird als »Hidden Bit« bezeichnet.
So nun sind die Zutaten bekannt, jetzt kann man das mal an einem Beispiel demonstrieren. Nehmen wir mal die Zahl »23,125«; das Vorzeichen ist noch relativ einfach zu ermitteln, die Zahl ist positiv, dementsprechend ist das Vorzeichen-Bit »0«. Um nun diese reelle Zahl in eine normalisierte binäre Zahl zu bringen, rechnen wir sie erst einmal in eine Festkommazahl um:
23,125
23 / 2 = 11 R 1 11 / 2 = 5 R 1 5 / 2 = 2 R 1 2 / 2 = 1 R 0 1 / 2 = 0 R 1 ↑ 0,125 * 2 = 0,25 → 0 ↓ 0,25 * 2 = 0,5 → 0 0,5 * 2 = 1,0 → 1 0,0 * 2 = 0,0 → 0
Somit haben wir das Zwischenergebnis »10111,0010«, welches nun noch normalisiert werden muss. Um nur eine Ziffer (≠ 0) vor dem Komma stehen zu haben, muss dass Komma um vier Stellen nach links verschoben werden, dass entspricht einer Multiplikation mit »24«. Für die normalisierte Darstellung erhalten wir demnach: 1,0111001 * 24. Die Mantisse wird nun ohne der ersten »1« gespeichert (»hidden bit«) und ergibt somit: 0111001, die restlichen Stellen, werden mit Nullen aufgefüllt.
Der Exponent ist »410«, was »1002« entspricht. Nun wird noch der »Bias« (127) auf den Exponenten addiert: 410 + 12710 = 13110 = 100000112. Setzt man nun diese ermittelten Werte zusammen kommen wir zu folgendem Ergebnis:
Die Erklärung unseres Problems
Wenn wir jetzt zu unserem eingangs erwähnte Problem zurückkehren und die Frage beantworten möchten, warum unsere Dezimalzahlen falsch ausgegeben werden können wir als mögliche Ursachen folgendes festhalten: Entweder haben wir es mit einer periodischen binären Zahl zu tun oder wir haben einen Überlauf in der Mantisse, was beides ein Abschneiden der Zahl nach 23 Zeichen zur Folge hat und somit unausweichlich zu einem Rundungsfehler führt.
Schauen wir uns mal die Zahl »0,1« an. Die Vorkomma-Ziffer ist einfach zu berechnen, sie ist »0«. Die Nachkomma-Ziffer »0,1« wird nach og Umrechnung wie folgt in eine binäre Form gebracht:
0,1
0,1 * 2 = 0,2 → 0 ↓ 0,2 * 2 = 0,4 → 0 0,4 * 2 = 0,8 → 0 0,8 * 2 = 1,6 → 1 0,6 * 2 = 1,2 → 1 0,2 * 2 = 0,4 → 0 0,4 * 2 = 0,8 → 0 0,8 * 2 = 1,6 → 1 0,6 * 2 = 1,2 → 1 ...
Man erkennt schon dass das Ergebnis periodisch ist und somit quasi bis in die Unendlichkeit fortgeführt werden könnte aber wir haben für die Mantisse nur einen Platz von 23 Bit. Somit ergibt unsere binäre Festkommazahl:
0,00011001100110011001100…
Um zu einer normalisierten Zahl zu kommen, muss das Komma um vier Stellen nach rechts verschoben, was einen Exponenten von »2-4« entspricht. So kommen wir auf Zwischenergebnis:
1,10011001100110011001100… * 2-4
Da »IEEE 754« ein »hidden bit« vorsieht ergibt die 23-stellige Mantisse:
10011001100110011001100
Da es sich aber um eine periodische Zahl handelt, wird nach »IEEE 754« nach dem mathematischen Prinzip gerundet. Dadurch wird das letzte Bit der Mantisse »0« auf »1« gerundet, was folgende endgültige Mantisse ergibt:
10011001100110011001101
Zu dem Exponenten wird noch das Bias hinzu addiert:
12710 - 410 = 12310 = 011110112
Das Vorzeichen ist »0«, da die Zahl positiv ist. Das ergibt somit folgende Darstellung:
Schlagen wir abschließend nochmal eine Rolle rückwärts und lösen die nun gewonnene binäre Gleitkommazahl in eine Dezimalzahl um.
- Vorzeichen: Wir haben eine »0« als Vorzeichen, was bedeutet unsere Zahl ist positiv.
- Exponent: Wir haben einen binären Exponenten von »01111011«, was dezimal der Zahl »123« entspricht. Von dieser Zahl muss jetzt noch ein Bias von »127« abgezogen werden, was einen Exponenten von »-4« ergibt.
- Mantisse: Die Mantisse hat zuzüglich dem weggelassenen hidden bit den Wert »1,10011001100110011001101«
Daraus folgt die normalisierte binäre Gleitkommazahl:
1,10011001100110011001101 * 2-4
Welche folgende binäre Festkommazahl ergibt:
0,00010011001100110011001101
Wenn wir diese Binärzahl jetzt in eine Dezimalzahl umrechnen, haben wir bei der Vorkommastelle kein Problem, den eine binäre »0« ist auch eine dezimale »0«. Die Nachkommastellen hingegen sind etwas aufwändiger zum umrechnen:
0,00010011001100110011001101
Der Nachkommateil 0,000110011001100110011001101 wird ins Dezimalsystem umgewandelt:
1 * 1 = 1
0 * 2 = 0
1 * 4 = 4
1 * 8 = 8
0 * 16 = 0
0 * 32 = 0
1 * 64 = 64
1 * 128 = 128
0 * 256 = 0
0 * 512 = 0
1 * 1024 = 1024
1 * 2048 = 2048
0 * 4096 = 0
0 * 8192 = 0
1 * 16384 = 16384
1 * 32768 = 32768
0 * 65536 = 0
0 * 131072 = 0
1 * 262144 = 262144
1 * 524288 = 524288
0 * 1048576 = 0
0 * 2097152 = 0
1 * 4194304 = 4194304
1 * 8388608 = 8388608
0 * 16777216 = 0
0 * 33554432 = 0
0 * 67108864 = 0
--------
13421773
Abschließend teilt man dann diese Summe durch die nächste Potenz der Basis 2:
13421773 : 134217728
13421773 : 134217728 = 0,100000001490116119384765625
…und addiere den bereits ermittelten ganzzahligen Anteil 0:
Addition der Vorkommastelle
0,100000001490116119384765625
+ 0
-----------------------------
0,100000001490116119384765625
Somit hätten wir den dezimalen Wert ermittelt, welcher sich ergibt, wenn die Zahl 0,110 in eine binäre Gleitkommazahl und wieder zurück in eine dezimale Zahl umgerechnet wird:
0,100000001490116119384765625
Bei dem fett markierten Teil handelt es sich um das Ergebnis, welches wir eingangs durch das Programm »float_3.c« mit neun Nachkommastellen erhalten haben. Wenn wir jetzt unser Programm so umschreiben, dass wir zB 30 Nachkommastellen ausgegeben bekommen, sollte das praktische Ergebnis mit dem theoretisch ermittelten übereinstimmen:
float_4.c
include <stdio.h> float f = 0.1; int main( void ) { printf( "%.30f\n", f ); }
$ ./float_4
0.100000001490116119384765625000
Sonderfälle
(Die Auflistung der Sonderfälle wurde übernommen von der FH Flensburg1))
Denormalisierte Zahlen und Null
Ein Sonderfall tritt auf, wenn der Exponent nur aus Nullen besteht. Dann wird bei der Mantisse keine implizite 1 vor dem Komma angenommen, sondern eine implizite 0. Zum Ausgleich beträgt der tatsächliche Wert des Exponenten in diesem Fall nicht -127, sondern -126. Auf diese Weise lassen sich noch betragskleinere Zahlen darstellen, bis hin zur 0. Die Zahl 0 wird also dargestelt durch lauter Nullen im Exponenten und lauter Nullen in der Mantisse; das Vorzeichen kann + oder - sein. Zahlen mit lauter Nullen im Exponenten werden als denormalisierte Zahlen bezeichnet.
Undendlich
Ein weiterer Sonderfall tritt auf, wenn der Exponent nur aus Einsen besteht. Besteht die Mantisse nur aus Nullen, so ist der Wert der dargestellten Zahl +∞ oder -∞, je nach Vorzeichenbit. Das Ergebnis +∞ ergibt sich, wenn eine positive Zahl durch 0 dividiert wird, oder bei einem Exponentenüberlauf.
NaN
Besteht der Exponent nur aus Einsen und enthält die Mantisse Einsen, so ist der Wert der dargestellten Zahl NaN (not a number). Dieser Wert ergibt sich u.a. als Ergebnis einer undefinierten Rechenoperation, wie z.B. 0/0 oder ∞ - ∞.
Folgende Tabelle stellt diese Sonderfälle dar:
| v | e | m | Wert |
|---|---|---|---|
0 | 0000 0000 | 000 0000 0000 0000 0000 0000 | +0 |
1 | 0000 0000 | 000 0000 0000 0000 0000 0000 | -0 |
0 | 1111 1111 | 000 0000 0000 0000 0000 0000 | +∞ |
1 | 1111 1111 | 000 0000 0000 0000 0000 0000 | -∞ |
? | 1111 1111 | 010 0110 0000 0000 0000 0100 | NaN |
— pronto 2011/11/30 00:50